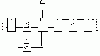При экспериментальной проверке способности человека к самообучению и выбору оптимальных алгоритмов, точно дозированных по количеству информации и сложности, была использована установка, блок-схема которой показана на рис. 1.
Вход автомата (блок 1) представляет собой клавиатуру из двоичных входов Х, с помощью которой испытуемый воздействует на автомат. Из первого блока сигнал поступает в коммутатор (блоки 2), где зафиксированы внутренние состояния автомата. Переключение внутренних состояний осуществляется селектором (блок 3), который управляется или испытуемым через входы, или экспериментатором (блок 7). Далее сигнал поступает в перекодирующее устройство (блок 4), где двоичные числа преобразовывают в десятичные. Затем он попадает на коммутатор 5, аналогичный блокам 2, и отображается на экране дисплея в виде десятичных цифр (выходы автомата Y). Приведенная модель обладала огромным разнообразием, которое было равно факториалу 5! на входе и 32! на выходе.
Такого количества вариантов нельзя реализовать ни в одной учебной задаче.
У автомата было шесть входов Х, из которых входы 1-5 позволяли вводить двоичные цифры, а шестой вход - изменять отображение двоичных цифр на десятичные и тем самым изменять структуру лабиринта.
Рис. 1 Блок-схема дискретного конечного автомата
Если испытуемый обучался алгоритму на автомате без памяти, то это порождало линейную кривую сенсомоторного обучения. При двух отображениях (включено два блока 2) – иногда возникал волновой процесс обучения. На рис. 2 показаны результаты самообучения трех человек на автомате с памятью. У второго испытуемого волны обучения наиболее заметны. Естественное объяснение появления волн – переучивание вследствие того, что испытуемый сам спонтанно переключал внутренние состояния автомата через один из входов. По-существу наша установка воспроизводила лабиринт: при использовании автомате без памяти он был постоянной структуры, а с памятью – переменной. Именно последнее и позволяло воспроизводить колебательный режим самообучения.
Рис. 2 Результаты самообучения трех испытуемых на модели лабиринта с переменной структурой (конечный автомат с памятью)
Сама методика эксперимента была такой. Испытуемый получал инструкцию: «На панели прибора находится 32 лампочки и шесть переключателей, с помощью которых вы должны научиться безошибочно зажигать лампочки в порядке возрастания номеров от 0 до 31. Одновременно можно использовать только один переключатель. Порядок работы с переключателями и темп вы устанавливаете сами. При включении очередной целевой лампочки нужно назвать ее номер. О всех промежуточных включениях говорить не нужно». После уяснения цели опыта испытуемый тренировался несколько минут для получения навыка работы с переключателями, затем эксперимент начинался. Никаких подкреплений со стороны экспериментатора не давалось. Весь ход опыта фиксировался на многоканальном самописце. Между отдельными опытами испытуемым иногда задавались вопросы с целью получения информации по уровню осознания процесса самообучения.
Интересно отметить, что ни один из трех испытуемых не смог выбрать оптимальный алгоритм решения задачи. Это полностью подтвердило гносеологический принцип А. Н. Колмогорова, который он изложил в письме к автору этой статьи: « Можно думать, что сопровождающее восприятие художественного произведения (и хорошего математического доказательства) ощущение красоты, законченности, основано на том, что вблизи предложенного автором решения нет лучшего. Достаточно интеллигентный слушатель музыки или читатель литературного произведения путем неосознанных проб ощущает это непосредственно – видит, что каждая нота, каждое слово «на своем месте» и не может быть заменено другим. Но отсутствие лучших решений, построенных совсем иначе, таких других лучших решений, которые не могут быть получены из предложенного путем постепенных мелких улучшений, лежит за пределами того, что может уловить самая изощренная наша «интуиция».
Поэтому, в качестве универсального принципа, руководящего работой мышления и творчества, остается лишь тенденция к поискам возможно более простых решений» (письмо А. Н. Колмогорова от 27 августа 1963 г.). Интересно отметить, что гносеологический принцип А. Н. Колмогорова оказался аналогичным принципу управления нелинейными системами (путем незначительных малых возмущений). Как утверждает А. С. Дмитриев [2], составные части таких систем никогда не достигают равновесия, а вместо этого эволюционируют от одного метастабильного состояния к другому. Подобное явление обнаружено и при обучении нейронных сетей [1] . Складывается впечатление, что в природе действует гносеологический принцип эволюции систем, который гений А. Н. Колмогорова предвосхитил удивительно точно. Отметим кстати, что распространение гносеологических принципов гуманитарных наук на естественные - вполне современная тенденция, которую достаточно подробно изложил Ю. М. Плюсин [6].
Эксперименты также позволили измерить и скорость самообучения человека, которая находится в диапазоне 19-220 бит в час. Это очень маленькая величина по сравнению с пропускной способностью различных анализаторов. Такой широкий диапазон скоростей самообучения вызван факторами сложности задач [5]. В лабиринтах с переменной структурой основной помехой, которая препятствует выбору оптимального алгоритма, оказалось явление инвариантности (в некоторых случаях при воздействии на вход «черного ящика» значения на выходе не меняются, хотя при этом происходит изменение структуры лабиринта). По-видимому, человек находится во власти «функционального мышления», а инвариантность в таком случае блокирует исследовательскую деятельность.
На первый взгляд маленькая скорость самообучения является недостатком мозга, однако природа не так уж недальновидна. При высоких скоростях эволюции какого-нибудь вида (самообучение можно считать родственным явлением процесса адаптации к новой среде) можно нанести непоправимый вред другому виду. Например, быстрая мутация вируса птичьего гриппа весьма опасна для человечества.
Устарел ли подход к исследованию поведения человека в нормированных по сложности и количеству информации средах в лабиринтах с переменной структурой? На наш взгляд не совсем. Возможно, метод лабиринтов с переменной структурой в современном оформлении заинтересует исследователей по педагогической психологии.
Литература
1. Ашкинази Л. Второе пришествие бионики.//Химия и жизнь. 2005. № 2. C. 22-24.
2. Дмитриев А. С. Детерминированный хаос и информационные технологии.// Компьютерра. 1998. № 47. С. 44-46. 3. Лившиц В. М. К вопросу об оптимальности форм мышления.//Ученые записки Тартуского Гос. Ун-та. Труды по философии. 8. Тарту. 1965. С. 55-64.
4. Лившиц В. М. Экспериментальное исследование самообучения человека на модели дискретного конечного автомата: Канд. дис. Л., 1967.
5. Лившиц В. М. Скорость переработки информации и факторы сложности среды.// Уч. записки Тартуского гос. ун-та. Тр. по психологии. Т. 4. 1976. № 4. С. 139-164.
6. Плюсин Ю. М. Проблемы биосоциальной эволюции. Новосибирск: Наука. 1990.