Способность человека перерабатывать информацию в настоящее время не может быть оценена с достаточной точностью, т. к. само это понятие не имеет устоявшегося научного определения в психологии. По крайней мере, следует согласиться с А. Ньюэллом, Дж. Шоу и Г. Саймоном [1], что человек обладает ограниченной способностью к переработке информации. Эти же авторы указывают, что способность человека к переработке информации можно повысить, например, путем увеличения мощности языка.
Способность человека перерабатывать информацию зависит от многих факторов и, прежде всего, от сложности той задачи, к которой он адаптируется. Тут следует согласиться с Л. Фогелем и др. [2], что сложность является многомерной величиной. К сожалению, пока нельзя указать все факторы, обуславливающие сложность задачи человека. В работах по экспериментальной и, особенно по инженерной психологии, имеются разные мнения на этот счет.
Л. Н. Ланда [3] предлагает оценивать сложность алгоритмов по среднему числу операций. В работах В. Н. Пушкина [4, 5] сложность алгоритмов оценивается по двум факторам: по числу операций и степени организации их структуры. В уже упомянутой работе [2] авторы исходят из "атомистического" принципа оценки сложности графа.
Несколько другой подход к проблеме сложности осуществил О. К. Тихомиров [6], который показал, что объективной сложностью для человека в шахматных задачах является степень конфликта между конечной и промежуточными целями игры.
В. М. Глушков в работе [7] предложил формулу для оценки сложности алгоритма (машина Тьюринга). Из этой формулы следует, что функция сложности включает три аргумента: длину алгоритма, число букв алфавита и количество различных состояний, которые может принимать головка машины Тьюринга.
В нашем исследовании ставилась задача оценить способность человека к переработке информации в информационных единицах и выявить некоторые факторы сложности среды.
Скорость переработки информации (W) можно расценивать в качестве количественного показателя успешности адаптации человека к среде при достижении им какой-нибудь цели. Численное выражение W приближенно можно получить из формулы:
W = &I/&t бит/(буква-час),
Где &I — приращение информации, &t — время адаптации.
Для экспериментальной оценки W необходимо подобрать подходящие среды, нормированные по сложности, и снять показатели процесса адаптации человека к среде в ходе реализации определенной цели. На рис. 1 — 5 показаны графы некоторых таких сред. Вершины графов соответствуют событиям, а ребра — операторам. Операторы q сред А1 … А4 (рис. 1 — 4) — двоичные, операторы среды А5 — троичные. Эти среды отличаются друг от друга некоторыми признаками. Так, среда А1 обладает инвариантом (inv. 1): ребра, отмеченные одним и тем же оператором, соединяют вершины графа с одинаковой разностью их номеров. Для q1 &n = 1, для q2 &n = 2 и для q3 &n = 4, где n — номер вершины. Среда А2 характеризуется другим инвариантом (inv. 2) — для перехода из вершины ni в ni+1 достаточно изменить состояние одного из трех операторов. В среде А3 нет инвариантов сред А1 и А2 . Среда А4 идентична среде А1 , но отображается в трехмерном пространстве. В среде А5 операторы имеют три состояния, и граф соответствует троичному коду десятичных чисел.
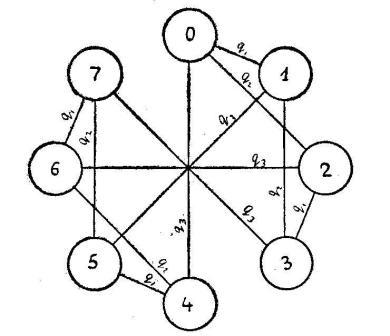
Рис. 1. Граф среды А1

Рис. 2. Граф среды А2
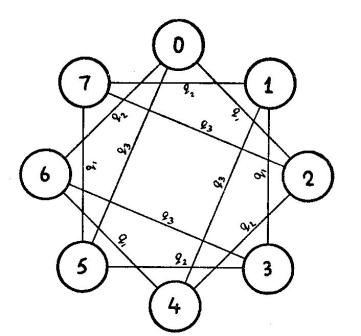
Рис. 3. Граф среды А3
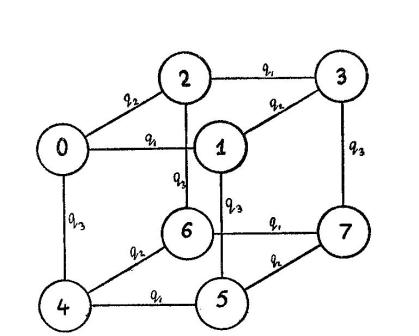
Рис. 4. Граф среды А4

Рис. 5. Граф среды А5
В качестве варьируемых свойств среды можно указать, например, на такие как число вершин графа, мерность оператора, инварианты, форма представления графа человеку и характер сигнала о состоянии графа (можно организовать непрерывную передачу информации человеку о состоянии среды или сообщать об этом дискретно в отдельные моменты времени).
Для определения W у человека и выявления факторов сложности среды можно использовать две методики для экспериментов:
- Предсказание человеком состояния среды и улучшение прогноза в процессе адаптации к среде.
- Обход вершин графа в заданном порядке и оптимизация алгоритма в процессе адаптации.
По первой методике испытуемым предлагалось угадывать числа в последовательностях. Последовательности составлялись по таблицам случайных чисел в соответствии с графами сред А1 и А5.
Проведено четыре серии опытов с группами испытуемых:
- Обучение предсказанию чисел в последовательности из 8 случайных чисел с условными переходами среды А1. Предъявление чисел вербальное, прогноз испытуемые делают вербально.
- Обучению предсказанию чисел в последовательности из 9 случайных чисел с условными переходами среды А5. Предъявление чисел и прогноз осуществлялись вербально.
- Обучение предсказанию чисел в последовательности из 8 случайных чисел с условными переходами среды А4. Перед испытуемым находилась модель среды в виде проволочного куба, вершины которого пронумерованы в соответствии с рис. 4. Предъявление чисел осуществлялось визуально — кратковременным высвечиванием их в соответствующих вершинах куба. Прогноз испытуемые делали вербально.
- Опыт аналогичен предыдущему, но с таким отличием: цифры, характеризующие состояние среды, высвечивались в течение всего времени нахождения графа в этом состоянии.
Результаты опытов по предсказанию испытуемыми чисел в последовательностях из случайных чисел с условными переходами даны в таблице 1.
Обсудим полученные результаты. Серия 1 и 2 имеют наименьшую W. Это можно объяснить тем, что при вербальном предъявлении чисел человеку приходится извлекать информацию из среды путем абстрактного мышления. Сама среда существует лишь в виде последовательности звуковых образов — слов. Равенство W для серии 1 и 2 указывает на то, что разная мерность операторов не оказывает заметного влияния на сложность среды.
Значительное увеличение W (в три раза!) в серии 4 по сравнению с серией 3 указывает на большое влияние характера сигнала состояния среды на ее сложность. При дискретном предъявлении сигнала человек, наблюдающий за средой, во-первых, должен запомнить, в каком состоянии находилась среда в момент ? - 1 и, во-вторых, сопоставить с состоянием среды в момент ?. Поскольку между двумя моментами времени проходило несколько секунд, то для извлечения информации испытуемому приходилось вовлекать сложные психические процессы мозга.
Таблица 1
| Серия опытов | W Бит/(буква-час) |
| 1 и 2 | 0.6 |
| 3 | 1.2 |
| 4 | 3.6 |
Вторая методика для определения W и выявления факторов сложности среды реализована на базе перекодирующего устройства, у которого имеется 6 или 5 двоичных входов (тумблеров) и 64 или 32 выхода соответственно. Выходом является табло в виде матрицы из оцифрованных лампочек. Каждому набору положений тумблеров на входе соответствует одна из лампочек на выходе. Во всех опытах перед испытуемыми ставилась задача научиться зажигать на табло лампочки по порядку номеров путем последовательного переключения тумблеров по одному. Проведено четыре серии опытов с группами испытуемых:
- Обучение сенсомоторному алгоритму на графе с 32 вершинами и 5 операторами. Каждая вершина соединена с пятью другими вершинами. Граф имеет inv. 1 и аналогичен среде А1.
- Обучение сенсомоторному алгоритму на графе с 64 вершинами и 6 операторами. Каждая вершина соединена с шестью другими вершинами. Граф имеет inv. 1 и аналогичен среде А1.
- Обучение сенсомоторному алгоритму на графе с 32 вершинами и 6 операторами. Каждая вершина соединена с пятью другими вершинами. Граф имеет inv. 2 и аналогичен среде А2.
- Обучение сенсомоторному алгоритму на графе с 32 вершинами и 5 операторами. Каждая вершина соединена с пятью другими вершинами. Граф не содержит inv. 1 и 2 и аналогичен среде А3.
Результаты опытов с испытуемыми по методике оптимизации сенсомоторного алгоритма даны в таблице 2.
Таблица 2
| Серия опытов | W Бит/(буква-час) |
| 1 | 6.9 |
| 2 | 6.6 |
| 3 | 5.1 |
| 4 | 0.7 |
Серия 1 и 2 имеют графы с одним и тем же инвариантом и различаются по числу вершин в графе. Графы серии 1 и 3 отличаются инвариантами. Граф серии 4 отличается от серии 1, 2 и 3 отсутствием инвариантов 1 и 2, что делает алгоритмы более сложными.
Из таблицы 2 видно, что отсутствие инвариантов значительно снижает W (почти в 10 раз!). Число же вершин графа и характер инвариантов не оказывает значительного влияния на сложность среды.
Выводы:
- Скорость переработки информации у человека для исследованных сред лежит в пределах 0.6… 6.9 бит/(час-буква) и зависит от сложности среды.
- Выявлено три фактора сложности среды для человека: форма представления, характер сигнала состояния и инварианты среды.
- Не подтвердилось предположение, что факторами сложности среды являются число вершин графа и мерность операторов.
Литература
- Ньюэлл А., Шоу Дж, Саймон Г. Программа для игры в шахматы и проблема сложности. - В сб. Вычислительные машины и мышление. М., "Мир", 1967.
- Фогель Л., Оуэнс А., Уолш М. Искусственный интеллект и эволюционное моделирование. М., "Мир", 1969.
- Ланда Л. Н. Алгоритмизация в обучении. М., "Просвещение", 1966.
- Пушкин В. Н. Об изучении мышления как процесса. - "Вопросы психологии", 1969, № 6.
- Пушкин В. Н. Психология мышления и принципы эвристического программирования. - "Вопросы психологии", 1967, № 6.
- Тихомиров О. К. Структура мыслительной деятельности человека. М., МГУ, 1969.
- Глушков В. М. Кибернетика и умственный труд. М., "Знание", 1965.
The rate of information treatment in the human mind and the influence of the environment complexity factors
V. Livshic
Summary
It was empirically shown that the speed of information processing is 0.6...6.9 bit /letter per hour and depends upon the complexity of the environment. There are three complexity factors: the way of environment presentation, the character of the environmental condition signal and the invariables of the environment. The number of developments and regularity of its operators until recently considered to be complexity factors were excluded as erroneous.