В работе Р. Шепарда и М.Тетцуняна рассматривалась способность испытуемых узнать повторяющееся число в ряду из предъявленных 200 чисел как функцию количества чисел между первым и вторым появлением числа в ряду. Было показано, что испытуемые легко справляются с заданием, пока это количество не превышает шести чисел, затем кривая эффективности узнавания монотонно снижается, приближаясь к нулевой отметке примерно при 40 промежуточных числах. Казалось бы, объем кратковременной памяти на числа измерен. Мы способны безошибочно воспроизводить ряд цифр, не превышающий 6 — 7 элементов.
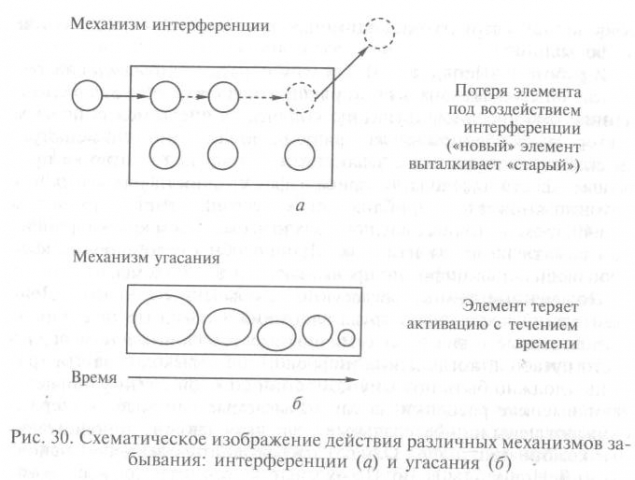
Полученные данные согласуются с обыденным опытом. Действительно, человек без труда запоминает обычные шестизначные почтовые индексы и семизначные телефонные номера, но часто путается, когда длина цифрового ряда выходит за эти границы (должно быть поэтому компании сотовой связи устанавливают высокие расценки на так называемые «прямые» номера и снижают цены на «федеральные», т.е. включающие дополнительные комбинации цифр). Однако эти результаты показались неполными Д. Норману и Н. Во. По их мнению, проведенное исследование не показывало, от чего именно зависит найденная закономерность: от количества поступивших в кратковременное хранилище цифр или от времени, которое прошло между предъявлениями. Другими словами, почему испытуемые не могут заметить, что целевая цифра уже встречалась им в ряду? Потому ли, что «новые» шесть цифр «вытесняют» находящиеся в кратковременном хранилище элементы, или потому, что, пока заучиваются «новые» элементы, «старые» исчезают под влиянием времени. Первый вариант связан с действием механизма интерференции, а второй — угасания (рис. 30).
Д. Норман и Н. Во в своем исследовании контролировали действие обеих переменных: и количество цифр между целевыми элементами, и время между первым и вторым предъявлением цифры в ряду. Они показали, что основным механизмом потери информации из кратковременной памяти является интерференция. Другими словами, «старая» информации, находящаяся в кратковременном хранилище, вытесняется вновь поступающей.
Использованная ими экспериментальная процедура была практически аналогична методике Р. Шепарда и М.Тетцуняна. Испытуемым предъявляли ряд из 16 цифр. Одна из цифр была «зондом». Она появлялась в списке дважды. Задача испытуемого заключалась в том, чтобы, услышав второй раз одну и ту же цифру, вспомнить цифру, которая предшествовала ей при первом предъявлении. Например, испытуемому давали ряд: 1, 2, 5, 7, 6, 3, 4, 5. Так как в данном случае зондом была цифра «5», правильный ответ — «2».
Если гипотеза о преобладании механизма интерференции в кратковременной памяти верна, то успех решения задачи должен зависеть от количества цифр, которые включены в ряд между цифрами-зондами, и не зависеть от скорости предъявления цифр. Действительно, в том случае, когда за равный промежуток времени испытуемому «успевали» прочесть различное количество цифр между цифрами-зондами (например, четыре или шесть цифр), он лучше справлялся с задачей при четырех «интерферирующих единицах», чем при шести. Однако эффект исчезал, когда интервал между предъявлениями приближался к 30 с. Таким образом, авторы пришли к выводу, что кратковременное хранилище структурно приспособлено к удержанию около шести элементов, которые, с одной стороны, подвержены интерферирующему воздействию вновь поступающей информации, а с другой — угасают в течение 30 с.
Что означает формула «шесть элементов»? Можно ли данные, полученные для цифрового и буквенного материала, распространить на слова, многозначные числа, осмысленные фразы и т.д.? Нам действительно трудно удержать в памяти цифровой ряд, превосходящий 6 —7 элементов, но мы легко можем запоминать многобуквенные слова (например, слово «достопримечательность» — 21 буква). Другими словами, на какой параметр поступающей стимуляции «настроено» кратковременное хранилище: на ее физические или какие-либо иные свойства? Очевидно, что перед нами встает вопрос об измерении «размера» элемента, который входит в кратковременную память.
Первая попытка подсчитать, сколько элементов способна вместить кратковременная память, восходит к классическим исследованиям объема сознания В. Вундта. В своих опытах по изучению объема сознания он установил, что объем сознания составляет около шести ассоциативно связанных объектов.
Способность человеческого сознания одновременно удерживать не более шести изолированных элементов, по мнению В. Вундта, была эмпирически обнаружена задолго до его исследований. Так, разработанный французским учителем XVIII в. Л.Брайлем алфавит для слепых кодирует каждую букву при помощи комбинации выпуклых точек. Каждый из символов в этом алфавите включал в себя не более шести точек (рис. 31). Таким образом, слепой мог одномоментно распознать букву, прикасаясь к конфигурации выпуклых точек.
Количественной мерой объема сознания для В. Вундта служил мелодический ряд, включающий различное количество тактов. Объем сознания определялся такой длиной ряда, что при последовательном прослушивании двух рядов испытуемый мог непосредственно установить их равенство. Он давал испытуемым прослушивать ряд, состоящий из одного, двух, трех, четырех и т.д. тактов. Такты могли быть различной степени сложности: двухдольные (тик-так), трехдольные (ритм вальса раз — два — три) и т.д. Испытуемым было запрещено специально сосчитывать количество тактов. Сразу после завершения одного ряда предъявлялся второй. Испытуемый должен был сказать, возникает ли у него ощущение равенства рядов или нет. Для этого нужно было сравнить удерживаемый в памяти ряд звуков с непосредственно воспринятым. Пользуясь современной терминологией, можно сказать, что процедура эксперимента предполагала сопоставление материала, находящегося в сенсорном регистре, с содержанием кратковременной памяти. Испытуемые давали верные ответы для восьми двухдольных, шести трехдольных и пяти четырехдольных тактов. Очевидно, что «количество информации», содержавшейся в этих тактах, было различным как по физическим параметрам (16, 18, 20 ударов соответственно), так и в отношении содержания (изолированный звук либо более или менее сложная мелодическая конфигурация). Таким образом, был зафиксирован факт, что человек способен удерживать в памяти единицы различной емкости. Но как сопоставить «информационную нагруженность» разнородных объектов? Что, например, окажется более нагруженным: геометрическая фигура или число; всегда ли информационно равны одинаковые по длине слова (например, «перекресток» и «университет»)?

Дж. Миллер в работе «Магическое число семь плюс или минус два. О некоторых пределах нашей способности перерабатывать информацию» предложил способ количественного измерения информации вне зависимости от того, в какой форме она представлена. В качестве меры информации им была введена так называемая двоичная единица информации, т.е. количество информации, необходимое для принятия решения о выборе из двух равновероятных альтернатив, в качестве условной меры информационной нагруженности. Что такое двоичная единица? Например, вам нужно догадаться, какого пола человек по фамилии Короленко. Человек, носящий такую фамилию, может с одинаковой вероятностью оказаться как мужчиной, так и женщиной. Для решения этой задачи вам понадобится одна двоичная единица (дв. ед.) информации, две дв. ед позволяют произвести выбор из четырех возможностей (например: на какую лапу прихрамывает собака?); три дв. ед. — из восьми возможностей (в каком направлении от Москвы находится Париж — на севере, юге, западе, востоке, юго-западе, северо-западе, юго-востоке или северо-востоке?); четыре дв. ед — из 16 возможностей (где выйдет пассажир, если он сел на станции «Университет» Московского метрополитена на поезд в направлении центра?); пять дв. ед. — из 32 возможностей (какой зуб может заболеть?) и т.д.
Сначала Дж. Миллер рассматривал гипотезу, согласно которой кратковременная память вмещает только определенное количество двоичных единиц информации. При этом абсолютное количество элементов может быть различным, важно только, чтобы сумма их информационных нагрузок не превышала предельной емкости системы. Например, каждая десятичная цифра несет 3,3 дв. ед. (так как существует выбор из десяти альтернатив от 0 до 9). Известно, что мы можем удержать в среднем 7 цифр, т.е. 23 дв. ед. Каждая буква русского языка несет около 5 дв. ед (выбор из 32 альтернатив). Исходя из логики, изложенной выше, следовало бы предположить, что мы можем удержать не более 4,6 букв. Однако, как видно из рис. 32, гипотеза Миллера о стабильной информационной емкости подсистемы кратковременной памяти, проверенная в эксперименте Дж. Хайеса, не подтвердилась. Несмотря на то что объем запоминания снижается с девяти элементов для двоичных чисел (одна дв. ед. информации на элемент) до пяти элементов для односложных слов (десять дв. ед. информации на элемент), результаты далеки от предсказанных исходной гипотезой. Количество воспроизведенной информации не является постоянной величиной и почти линейно возрастает с увеличением поступающей информации, приходящейся на один элемент. Причем абсолютное число воспроизведенных элементов постоянно находится в диапазоне «магического числа 7 ± 2».

С учетом полученных данных Дж. Миллер приходит к выводу, что кратковременная память ограничена числом запоминаемых единиц, а не их информационной нагруженностью. Он вводит различение между количеством информации и «чанком» информации (от англ. chunk — ломоть, кусок). «Чанк» представляет собой своеобразную ячейку памяти, в которую можно поместить как «мало», так и «много» информации. «Поскольку объем памяти равен ограниченному числу ячеек, мы можем увеличить число двоичных единиц, приходящихся на одну ячейку информации, путем построения все больших и больших ячеек, причем так, чтобы каждая ячейка содержала больше информации, чем раньше» (Миллер Дж. — 1965. — С. 575). Очевидно, что в реальной жизни нам выгоднее оперировать с информационно богатыми, чем с информационно бедными элементами.
Процесс укрупнения ячеек Дж. Миллер называл перекодированием. Перекодирование — это процесс, в ходе которого ранее изолированные элементы объединяются в группы. Одним из наиболее экологически валидных примеров укрупнения ячеек кратковременной памяти является создание осмысленных слов из потока буквенной стимуляции.
Дж. Боуэр предъявлял на слух испытуемым ряды букв. Буквы произносились либо в постоянном темпе, либо с различными интервалами. Например, при монотонном предъявлении ряд мог иметь такой вид:
О-Б-С-Е-О-О-Н-Ю-А-Р-Е-Э-С.
В случае с варьируемыми паузами, ряд принимал следующую форму:
ОБС - ЕОО - НЮ - АРЕ - ЭС
или
ОБСЕ - ООН - ЮАР- ЕЭС.
Хотя число букв во всех трех рядах идентично, результаты воспроизведения в третьей серии были значимо лучше, чем в двух предшествующих. Дж. Боуэр связывал полученные результаты с тем, что совпадение со знакомыми акронимами (буквенными сокращениями) позволяло сформировать более богатые ячейки памяти.
Сходные данные были получены в исследовании А. Бэддели, Р.Конрада и У.Томсона по методике последовательных приближений буквенных комбинаций к естественным словам английского языка. С помощью компьютера было подсчитано, с какой частотой в нормальном тексте встречаются отдельные буквы и их сочетания. На основании выявленных частот были созданы десятибуквенные ряды, изменяющиеся от случайного набора к приближению первого порядка (буквы встречаются с характерной для языка частотой), потом к приближению второго порядка (пары букв встречаются с типичной частотой), потом к приближению третьего порядка (типичная частота троек букв) и, наконец, реальные слова языка. Так, примером комбинации букв случайного набора может служить ряд RCIFODWVIL, примером приближения первого порядка — TNEOOESHH, примером приближения второго порядка — HIRTOCLTNO, примером приближения третьего порядка — BETEREASYS, примером реального слова — PLANTATION (плантация). Было установлено, что вероятность безошибочного воспроизведения буквенного ряда возрастает с приближением к словам естественного языка (рис. 33). Данный феномен получил название эффект лексичности (lexicality effect).

Явление укрупнения элементов, помещаемых в ячейки кратковременной памяти, было продемонстрировано и на материале целостного текста. Э.Тульвинг и Дж. Пэтко использовали списки из 24 слов, которые также различались по своей близости к осмысленному тексту. Число припоминаемых слов находилось в прямой зависимости от порядка приближения к литературному тексту. Испытуемые воспроизводили пять-шесть структурных элементов, объем которых увеличивался от одного до трех слов по мере нарастания совпадения с устойчивыми синтаксическими конфигурациями языка. Они ввели понятие заимствованная структурная единица, которая отражает наличие в долговременной памяти, стабильной группы стимулов. Эти стимулы опознаются как целое, безошибочно воспроизводятся в правильном порядке, и, соответственно, имеется возможность их заимствования для обеспечения процесса структурирования содержаний в кратковременной памяти. Например, для запоминания текста вида: «Она вышла из дома ровно в пять» — требуется четыре заимствованные единицы («она», «вышла», «из дома», «ровно в пять»), а для запоминания текста вида: «Из пять в вышла она дома» — уже шесть единиц, так как каждое слово в данном случае должно будет распознаваться изолированно.

Правило, согласно которому объем кратковременной памяти не зависит от количества информации в отдельном элементе, а определяется постоянным числом ячеек памяти, которые могут быть как богаты, так и бедны информацией, действует в достаточно широких пределах. Однако, как и всякое правило, оно имеет ограничения. Нельзя увеличивать информационную нагрузку ячейки памяти до бесконечности. Математическая зависимость, связывающая объем кратковременной памяти и абсолютное количество содержащейся в запоминаемом материале информации, была описана П. Б. Невельским. Он установил, что данная зависимость носит линейный характер, причем при обогащении элементов информацией в 40 раз (с 0,5 до 20 дв. ед.), количество структурных единиц, с которым могла оперировать кратковременная память, сокращался только в четыре раза (с 12 до 3) (рис. 34).








